1. 문제
https://www.acmicpc.net/problem/9370
2. Note
2.1. 풀이
저는 Dijkstra를 세 번 사용하여 풀었는데 Dijkstra를 두 번, 심지어는 한 번만 사용해도 풀 수 있습니다. 한 번만 푸는 풀이법은 금방 이해했는데 두 번만에 푸는 풀이는 이해하는데 조금 시간이 걸려서 메모합니다.
2.1.1. 두 번 사용하는 풀이
u->v := u에서 v까지의 최단 경로
(u,v) := u와 v를 잇는 간선
dist(u,v) := u부터 v까지의 최단 거리
length(u,v) := (u,v)의 길이
먼저 s->d가 (h,g)를 포함한다고 가정합니다.
그렇다면 dist(s,h) < dist(s,g)일 때 dist(s,d) = dist(s,h) + length(h,g) + dist(g,d)입니다.
증명
s->g + (h,g) + h->d의 거리가 s->h + (h,g) + g->d보다 짧다고 가정해봅시다.
즉, dist(s,g) + length(h,g) + dist(h,d)가 최단 거리입니다.
그렇다면, dist(s,h) + dist(g,d) > dist(s,g) + dist(h,d)입니다.
또한, dist(s,h) < dist(s,g)이므로 적어도 dist(h,d) < dist(g,d)입니다.
결론적으로 dist(s,g) + length(h,g) + dist(h,d) > dist(s,h) + dist(h,d)이 성립합니다.
따라서 dist(s,g) + length(h,g) + dist(h,d)가 최단 거리라고 가정했는데도 이것보다 짧은 거리의 경로가 존재합니다.
이는 모순이므로, s->g + (h,g) + h->d는 최단 경로가 아닙니다. 즉, s->h + (h,g) + g->d가 최단 경로입니다.
2.1.2. 한 번 사용하는 풀이
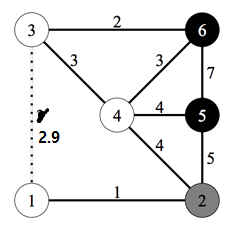
... 원래 가능한 도착지가 아니었다면, 점선의 거리가 0.1 줄어든 것은 아무런 도움도 못 됩니다. 반면 가능한 도착지였다면, 무조건 저 점선을 선택해야 최단거리로 갈 수 있습니다. 그리고 그 때의 최단거리는 자연수가 아니게 됩니다!
[BOJ 9370] 미확인 도착지|작성자 jh05013
3. Reference
'Problem Solving' 카테고리의 다른 글
| [BOJ1208] 부분수열의 합 2 (0) | 2020.06.30 |
|---|---|
| [BOJ1248] 맞춰봐 (0) | 2020.04.22 |
| [BOJ12015] 가장 긴 증가하는 부분 수열 2 (0) | 2020.03.24 |
| [BOJ1300] K번째 수 (이분 탐색) (0) | 2020.03.23 |
| [BOJ2110] 공유기 설치 (0) | 2020.03.23 |